Paper Explain: "SORSA: Singular Values and Orthonormal Regularized Singular Vectors Adaptation of Large Language Models"

Table of Contents

See the original paper on arXiv.

Introduction
#

SORSA is a novel Parameter Efficient Fine-Tuning (PEFT) method for neural networks. SORSA uses Singular Value Decomposition (SVD) and Orthonormal Regularization to make the model converge faster and improve the generalization ability of the model. The core idea of SORSA is to ensure the Orthonormality of the singular vectors during training, making the singular values of the model more stable during the training process, thereby accelerating convergence and improving the generalization ability of the model.

The architecture of SORSA adapters is shown in the figure below:

Only the parts rendered in orange ( $U_p$, $\text{diag}(S_p)$ and $V^\top_p$) are trainable.

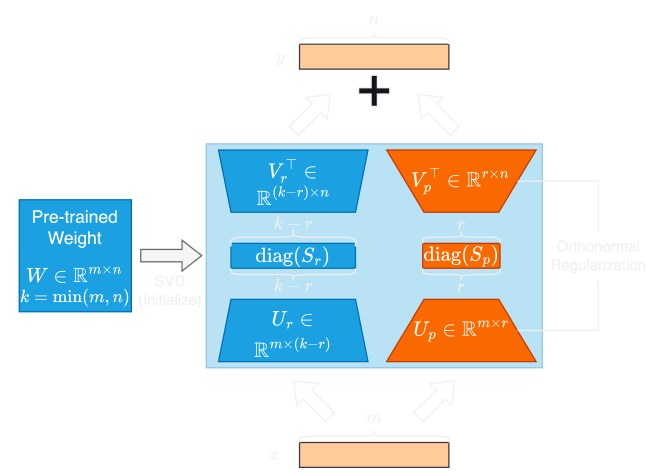
Training of SORSA
#

The Orthonormal Regularizer of SORSA can be expressed as: $$ \mathcal{L_{reg}} = || U_p^\top U_p - I ||_F + || V_p^\top V_p - I||_F $$ where $ ||W||_F $ denotes the Frobenius norm of $W$.

The gradient descent of SORSA can be divided into two steps: the loss update of SORSA and the Orthonormal Regularizer update of SORSA, which can be expressed as:

$$ W_{p,t+1} = W_{p,t} - \eta_{t} \nabla_{W_{p,t}} \mathcal{L_{reg}} - \gamma_{t} \nabla_{W_{p,t}} \mathcal{L_{reg}} $$ where $t$ is the training step, $W_{p} = U_p\text{diag}(S_p)V^\top_p$, $\eta$ is the learning rate, and $\gamma$ is the hyperparameter of the Regularizer of SORSA.

SVD Analysis
#

We analyzed the update process of SORSA. During the training process, SORSA has different patterns of changes in singular values and singular vectors compared to Fine-Tuning (FT) and LoRA.

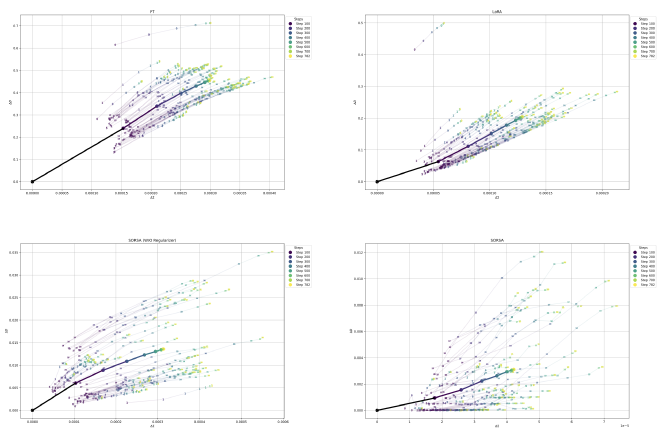
We can see that at the corresponding training steps, the average change in singular vectors $\Delta D$ and the average change in singular values $\Delta \Sigma$ of SORSA are the smallest among the four methods. This indicates that SORSA can retain the information of the original weights as much as possible.

At the same time, we can see that the update pattern of SORSA does not show a clear linear relationship between $\Delta D$ and $\Delta \Sigma$ as FT, LoRA, and the method without applying the Orthonormal Regularizer. This indicates that SORSA reduces the constraints on the singular values and singular vectors of the weights during parameter updates, allowing the model to explore and converge more efficiently.

Gradient Analysis
#

We have proven that the Orthonormal Regularizer of SORSA can continuously improve the condition number of the weights during the update process, thereby improving the speed and generalization ability of optimization. For more details, please refer to the Paper.

Experimental Results
#

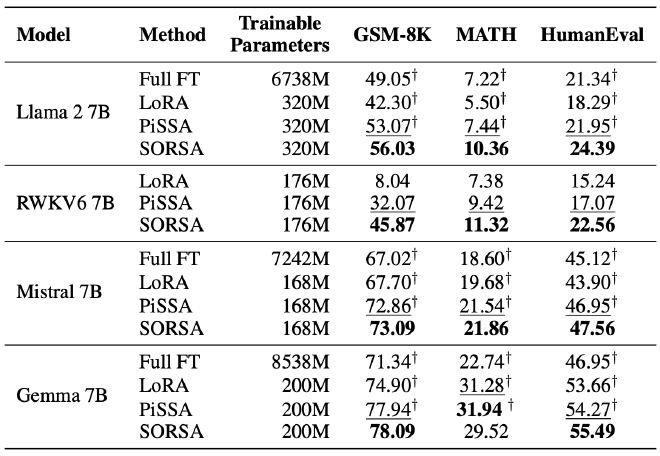
Experimental results show that SORSA achieves excellent performance on multiple datasets and significantly improves the performance of large language models. The experimental results are shown in the figure below: